Pola Mosaik Keramik Unik yang Menyatu Tanpa Replikasi Berkat Rumus Matematika

Berita Baru, Amerika Serikat – Pernah menginginkan pola keramik kamar mandi atau dapur unik yang sebenarnya? Nah, ahli matematika telah menemukan ubin yang sempurna untuk Anda.

Dilansir dari Dailymail.co.uk pada 12 April, Sebuah tim dari University of Arkansas telah menemukan bentuk pertama yang dapat menutupi dinding tanpa pernah membuat pola berulang.

Properti ini dikenal sebagai ‘ubin aperiodik’, dan hingga saat ini hanya dapat dicapai dengan menggunakan lebih dari satu bentuk.

Tapi yang satu ini, dijuluki ‘topi’, mampu menyatu dengan dirinya sendiri untuk menghasilkan pola yang tak terbatas dan meluas.

Ia bahkan mempertahankan kemampuan ubin aperiodiknya ketika 13 sisi bentuk diubah panjangnya, memberikan kemungkinan lebih banyak pola.

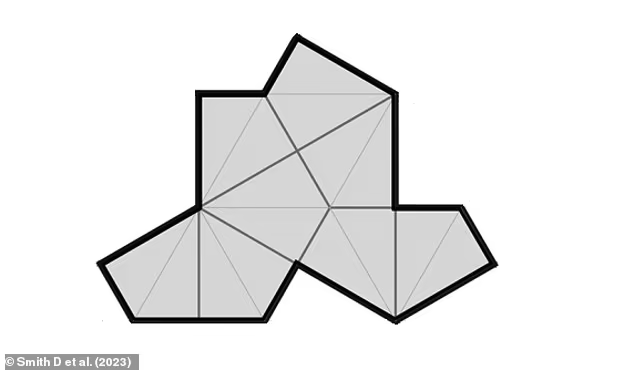
Ubin mengacu pada menutupi permukaan datar dengan bentuk yang cocok satu sama lain tanpa ada celah atau tumpang tindih. 

Ubin aperiodik adalah jenis ubin khusus di mana pola bentuk yang digunakan untuk menutupi permukaan tidak berulang. 

Ini berbeda dengan ubin periodik, yang menggunakan bentuk untuk menutupi permukaan dalam pola yang berulang secara teratur, seperti segitiga dan bujur sangkar.

Kumpulan bentuk pertama yang dapat menciptakan pola yang tak terbatas dan berbeda secara bersamaan ditemukan pada tahun 1963 oleh matematikawan Amerika Robert Berger.

Ini terdiri dari 20.426 bentuk unik, tetapi temuan tersebut memicu penelitian lebih lanjut tentang ubin aperiodik, untuk melihat apakah angka tersebut dapat diturunkan.

Kumpulan ubin aperiodik yang paling terkenal dikenal sebagai ‘ubin Penrose’, yang terdiri dari dua bentuk belah ketupat yang berbeda dan diterbitkan pertama kali pada tahun 1974.

Sejak saat itu, ahli matematika telah mencari ‘einstein’ yang sulit dipahami; bentuk yang dapat mencapai ubin aperiodik dengan sendirinya.

Pada tahun 2010, sebuah tim dari Universitas Duke mengklaim bahwa mereka telah menemukan bentuk yang sesuai dengan tagihan, namun diperlukan penggunaan ubin plus gambar cerminnya. 

Mereka memang menunjukkan bahwa itu juga mungkin untuk mencapai pola ubin aperiodik tanpa bentuk yang dipantulkan, tapi ini dalam tiga dimensi, bukan bidang tunggal. 

Untuk studi setebal 89 halaman mereka, yang diterbitkan di arXiv , para peneliti yang berbasis di Fayetteville akhirnya bertujuan untuk menemukan einstein yang sebenarnya, yang berarti ‘satu batu’ dalam bahasa Jerman.

‘Sudah lama menjadi pertanyaan terbuka apakah ubin seperti itu ada,’ tulis mereka. 

Tim pertama kali menggunakan komputer untuk menyaring ratusan bentuk yang berbeda, menghilangkan yang jelas tidak sesuai dengan tagihan.

Mereka kemudian melihat lebih dekat pada bentuk yang dilontarkan sebagai einstein potensial, dan mencoba membuktikan secara matematis bahwa mereka akan menghasilkan ubin aperiodik.

‘Anda benar-benar mencari satu dari sejuta hal,’ kata penulis utama Dr Chaim Goodman-Strauss kepada New Scientist .

“Anda memfilter 999.999 yang membosankan, lalu Anda mendapatkan sesuatu yang aneh, dan kemudian itu layak untuk ditelusuri lebih lanjut.”

“Dan kemudian dengan tangan Anda mulai memeriksanya dan mencoba memahaminya, dan mulai menarik keluar strukturnya.”

“Di situlah komputer menjadi tidak berharga karena manusia harus terlibat dalam menyusun bukti yang dapat dipahami manusia.”

Pada akhirnya, penulis pertama David Smith yang akhirnya menemukan topi tersebut, ‘hanya dengan menjelajahi bentuk-bentuk menarik dengan tangan, menggunakan rasa dan intuisi’.

“Untungnya, pekerjaan kami sebelumnya berarti bahwa kami memiliki perangkat lunak yang berperan penting dalam menunjukkan bahwa topi berperilaku seperti itu,” kata rekan penulis Dr Craig Kaplan kepada media.

Mereka benar-benar berhasil membuktikan aperiodisitas topi itu dua kali.  

Para matematikawan berharap pengetahuan tentang bentuk unik mereka akan mengarah pada penciptaan materi baru yang lebih kuat, atau memiliki sifat berguna lainnya.

Pola berulang sering terlihat pada struktur molekul bahan kristal, dan membuatnya mudah pecah.

‘Topi itu memicu imajinasi seperti halnya ubin tidak biasa lainnya,’ kata Dr Kaplan kepada media. 

“Jadi, penerapan yang paling cepat adalah pada seni.”

“Saya telah melihat orang bereksperimen dengan mendekorasi topi untuk menghasilkan desain seperti Escher, dan banyak orang berspekulasi tentang menata ulang lantai kamar mandi mereka dengan topi!”